高速ゼータ変換(FZT)
コードについての説明
ゼータ変換は以下の 2 種類のことを指して呼ばれる.
(1) $s$ を含むような上位集合 $T$ についての $f(T)$ の総和
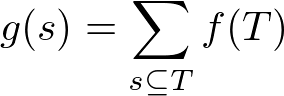
(2) $S$ に含まれる下位集合 $t$ についての $f(t)$ の総和
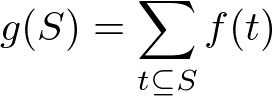
このとき $g$ は $f$ のゼータ変換でありこのような $g$ は計算量 $\O (n2^n)$ で求めることができ, 実装自体は以下のようにシンプルにかける(in-place で実装しているので少し分かりにくい).
以下の実装の $i$ 番目のループでは上位 bit から見たときに下から $i$ bit 目で初めて $s$ と bit が異なるような $s$ を含む集合 $T$ について足しあげており, つまり
各ループ $i$ の終了時に $f(s)$ には下から $i$ ビット目より上位の bit については $s$ と同じ、下から $i$ bit 目までについては $s$ の上位集合となる要素の和が暫定の値として入っている.
よって各ループで足し合わせるべき値は 1 つ前のループまでの結果の $f$ を用いて更新できることが分かる.
ざっくり言えば $n$ 次元累積和テーブルを計算していることと同じ(順番に各次元の方向に足し合わせて結果を得る)
時間計算量: $\O (n 2^n)$
コード
// 上位集合(含む集合)の和
void fast_zeta_transform(int n, vector<int>& f)
{
for(int i = 0; i < n; ++i){
for(int j = 0; j < (1 << n); ++j){
if(!(j >> i & 1)) f[j] += f[j ^ (1 << i)];
}
}
}
// 下位集合(含まれる集合)の和
void fast_zeta_transform(int n, vector<int>& f)
{
for(int i = 0; i < n; ++i){
for(int j = 0; j < (1 << n); ++j){
if(j >> i & 1) f[j] += f[j ^ (1 << i)];
}
}
}
