Chromatic Number Algorithm

個人的メモ

(スライドの説明)
分かりやすく, "グラフ $G = (V, E)$ が $k$ 彩色可能 ⇔ $V$ を $k$ 個の独立集合で被覆可能" と言い換える. ここで各独立集合は disjoint とは限らないと定義しておく(こう定義しても同値性は変わらない).
このとき頂点集合 $S (\subseteq V)$ について $f_k(S)$ を $S$ に含まれる独立集合を $k$ 個選ぶ場合の数、 $g_k(S)$ を $k$ 個の独立集合を選んでその和集合が $S$ となるような場合の数とする.
包除原理から次の式が成り立つ.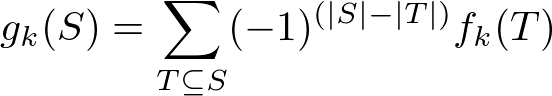
直接成り立つと考えてもいいし、 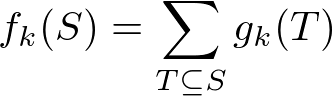は明らかに成り立つのでその逆変換(Mobius 変換) と考えても良い.
$I(S)$ を $S$ に含まれる独立集合の個数とすると, $f_k(S) = I(S)^k$ であり, $I(S)$ は $I(S) = I(S \setminus \{ v \} ) + I(S \setminus adj[v])$ の漸化式を用いて $\O (n 2^n)$ 時間で求めることができる. 漸化式は $v$ を含まない独立集合 と $v$ を含む独立集合を分けて数え上げている(注 $adj[v]$ は $v$ および $v$ に隣接する頂点集合とする).
最終的には $g_k(V)$ が非ゼロとなるような最小の $k$ が彩色数となる. 実装を行う際はオーバーフローを避けるため大きい素数 $p$ を用いた $\mathbb{Z}_p$ 上で計算を行う.