Directed Minimum Mean Weight Cycle Algorithm

個人的メモ

便宜上証明では元のグラフに超頂点 $S$ と $S$ から各頂点に重み $0$ の辺を張ったグラフを新たに $G$ とおいてグラフ $G$ に含まれる最小平均長閉路を求めることにする. 新たに頂点, 辺を加えたことで閉路が増えることはないのでこの変換によって解は変化しない.
$F_k(x)$ を始点を $s$, 終点を $x$ とする長さ $k$ の walk の最小の重みとする. walk は頂点及び辺の重複を許すパスとする. また長さ $k$ の walk とは $k$ 本の辺からなる walk の意味で使っています. もしそのような walk が存在しなければ $\infty$ と考える. このとき $\mu (G, c)$ をグラフ $G$, 重み関数 $c$ に対する最小平均長閉路の値とすると以下の重要な等式が成り立つ.

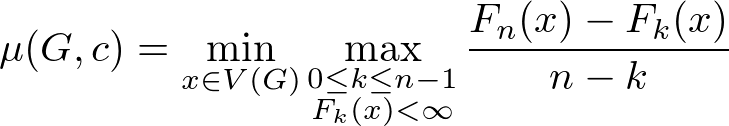
アルゴリズム自体はこの等式が成り立つことがすべてなんだけど, この等式まあまあ非自明な気がする.
まず以降 $G$, $V(G)$, $n (= |V(G)|)$ はすべて超頂点 $S$ およびそれに付随する辺を含んでいるものとして考えることにする.
最初に

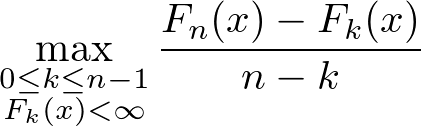
が $\mu(G, c)$ 以上であることを示す.
$F_n(x)$ は長さ $n$ の walk であることからその道中で少なくとも $1$ つの頂点を $2$ 度以上通る.
最後に $2$ 度以上通った頂点を $t$ としてそれが長さ $n$ の walk の $j$ 番目とする. また $j$ 番目より前かつ一番最後に $t$ を通ったときを $i$ 番目とする. このとき $F_n(x)$ に対応する長さ $n$ の walk $T$ のうち $x$ 番目から $y$ 番目までの部分ウォークを $T_{xy}$ と表すことにする. また $T_{0i}, T_{jn}$ のようにたどった長さ $n + i - j$ の walk の重みを $W$ とする. ここで $T_{ij}$ のループの平均重みは $\mu (G, c)$ 以上, $W$ は $F_{n+i-j}(x)$ 以下であるという事実から

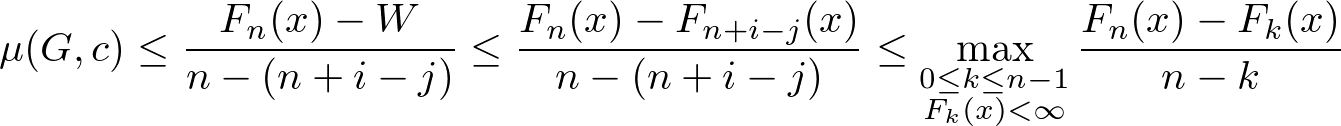
が成り立つので示せた.
次に上式がすべて等号で成り立たつような頂点 $x$ が存在することを示そうとしたが, ここで全辺の重みを $- \mu (G, c)$ して $\mu (G, c) = 0$ の場合のみ考えれば十分あることが参考書を見てわかったのでその方針で示すことにする (このままやるとかなり証明がややこしくなり, 参考書を見るとこの方針でやっていた. たぶん上記の 1 つ目の証明も "$0$ 以上であることを示す" に限定して考えたほうが楽そう). ちなみに示すべき等式の両辺が等しく $- \mu (G, c)$ されるのでこの十分性は正しい.
最小平均長を達成する有向閉路を $C$ として, $C$ 内のある頂点 $w$ について最短距離に対応する walk $P_{sw}$ を考える. 以降, 有向閉路 $C$ 上の頂点 $x$ から $y$ への(辺の重複を許さない)パスを $C_{xy}$ と表すことにする. $\mu (G, c) = 0$ で負の有向閉路が存在しないことから最短距離は有限でかつ walk の長さは $n-1$ 以下である. 次に始点 $s$ から出発して $w$ に着いたあと $C$ 上を有向閉路の方向に沿って進み walk の長さが $n$ になったときの頂点を $x$ とする. ここで $P_{sx}$ は $s$ から $x$ への最短 walk となっていることが言える.
そうでないとすると $s$ から $x$ への walk $P'_{sx}$ で $P_{sx}$ よりも重みが小さいものが存在することになる(その重みを $c$ とする). また $P_{sw}$ の重みを $a$, 頂点 $w$ から $x$ への $C$ 上のパス $C_{wx}$ の重みを $b$ としたとき $c < a + b$ が成り立つ. ただ有向閉路 $C$ の長さ(重み)は $0$ なので頂点 $x$ から $w$ への $C$ 上のパス $C_{xw}$ の重みは $-b$ となり 始点 $s$, 終点 $w$ の walk $P_{sx} + C_{xw}$ についてその重みが $c - b(< a)$ となる. これは最短距離に対応する walk $P_{sw}$ の重みが $a$ であることに矛盾する. よって $P_{sx}$ は $s$ から $x$ への最短 walk となっていることが示せた.
最後にこれより $F_n(x) = dist(s, x)$ であることが分かり, また $\mu (G, c) = 0$ であることから長さ $n-1$ 以下の $s$ から $x$ までの最短パスが存在する. つまり $\underset{0 \le k \le n-1}{\min} F_k(x) = dist(s, x)$ が成り立ち, このような頂点 $x$ について上の式が等式で成り立つため結果的に最小平均長閉路の値に関する重要な等式が示せた.
実装はこの $F_k(x)$ を Bellman ford 法(DP) で求めて min max を計算したらおしまい.

(無向グラフの最小平均長閉路アルゴリズムについて)
補足ではあるが, 無向グラフの場合に上記の最小平均長閉路アルゴリズムを応用するため両方向に辺を張ると, 結局重み最小の辺に対応するループ(invalid なループ)が検出されるだけでうまく動かない.
調べると最小重みの $\emptyset$-join (Euler 部分グラフ) を求める問題を $\O (n)$ 回解くことで求められるらしいので計算量は $\O (n^4)$(詳しくはよくしらない).