Eldös Gallai's Theorem
コードについての説明
Eldös Gallai の定理はグラフの次数列が与えられたときにそれに対応する単純グラフが存在するかどうかの必要十分条件を与える定理である.
具体的には降順に並べた次数列 $d_1,\ldots,d_n$ の総和が偶数であることと以下の関係式が $1 \le k \le n$ について成り立つことが必要十分条件である.
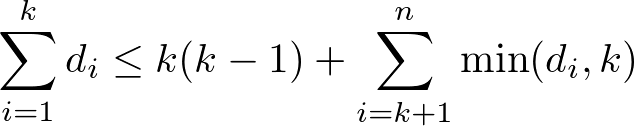
必要条件であることは難しくなく, 十分条件であることは Havel-Hakimi アルゴリズム + 帰納法を用いることで構成的に示すことができる.
(注)実装は std::sort を用いているため計算量は $\O (n \log n)$ である(バケットソートなどで $\O (n)$ time に改善できる).
(関数)
IsExist$(d)$: 次数列を引数に存在するかどうか (true / false) を返す.
時間計算量: $\O (n \log n)$ (バケットソートを用いれば $\O (n)$)
コード
bool IsExist(vector<int> d){
int n = (int)d.size();
vector<long long> sm(n+1, 0);
sort(d.begin(), d.end(), greater<int>());
for(int i = 0; i < n; i++) sm[i+1] = sm[i] + d[i];
if(sm[n] % 2) return false;
int pos = n-1;
for(int i = 0; i < n; i++){
while(pos >= 0 && d[pos] < i+1) pos--;
if(sm[i+1]>(long long)(i+1)*i+sm[n]-sm[max(i, pos)+1]+(long long)(i+1)*max(pos-i,0)){
return false;
}
}
return true;
}
