Articulation Node Find Algorithm(Constructing Block Cut Tree)
コードについての説明
関節点を求めるアルゴリズム. 加えて block cut tree の構築(二重頂点連結成分分解) も行う.
関節点とはその点を削除した場合にグラフが非連結になるような頂点のことで, lowlink という値を用いて線形時間で計算することができる. 橋の列挙 にも同様の手法が用いられる.
割ととっつきにくい概念だと思うのでこの記事やこのスライドを見るとわかりやすいかもしれない.
発展として lowpt1(高々1個の後退辺を通ってたどり着けるノードの行きがけ順の最小値)だけでなく, lowpt2(高々1個の後退辺を通ってたどり着けるノードの行きがけ順の2番目の値) も合わせて計算しておくことで
3(点)連結成分のようなものを求めることができ, この考えが Hopcroft, Tarjan の線形時間でのグラフの平面性判定アルゴリズム("Efficient Planarity Testing" [Hopcroft, Tarjan 1974]) に用いられている.
(補足)
(block cut tree の特徴)
(1) cut node はグラフの関節点と対応する.
(2) block node はグラフの $2$ 点連結成分と対応する($1$ 本の辺のみからなるグラフを $2$ 点連結と考えた場合).
(3) 各辺はちょうど $1$ つの block node に含まれる.
(4) block cut tree の辺の両端点は片方が block node $b$, もう片方が cut node $c$ であり, その cut node $c$ は block node $b$ に対応する $2$ 点連結成分に含まれる.
(5) 元のグラフにおける次数 $1$ の頂点は関節点ではないため対応する cut node は存在しない. そのため block cut tree の葉はすべて block node である.
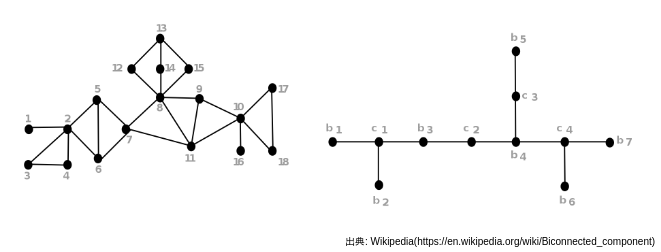
(block cut tree の例)
左が元のグラフで右がその block cut tree である.
(関数)
add_edge$(u, v)$: $u, v$ の間に無向辺を追加する
solve(): 関節点を求めて($art$ に true/false が入る), さらに block cut tree(forest) の構築を行いそのサイズを返す.
具体的に bctree が block cut tree の隣接リスト表現, bcnodes がその頂点集合で bcnode 型は isBlock(各頂点が block か cut か) と
component(block なら辺集合, cut ならサイズ 1 で要素は {関節点のインデックス, 関節点のインデックス}) から成る(いずれも元のグラフ上でのインデックス).
ここでは 1 頂点 0 辺からなる連結成分は block node でも cut node でもないと考える.
時間計算量: $\O (n+m)$
コード
// 多重辺に対応している.
// 自己ループは bc tree を定義する上で便宜上存在しないことを仮定している.
class Articulation {
public:
struct bcnode;
private:
const int V;
vector<int> ord, low;
bool check(const int u){
for(const int v : G[u]){
if(ord[v] < 0) return true;
}
return false;
}
void identify_block(const int u, const int v, bool *used,
stack<pair<int, int> >& st, const vector<int>& bcnode_id){
vector<pair<int, int> > block;
vector<int> cut_vertex;
while(!st.empty()){
const pair<int, int> p = st.top();
st.pop(), block.push_back(p);
if(art[p.first] && !used[p.first]){
cut_vertex.push_back(p.first);
used[p.first] = true;
}
if(art[p.second] && !used[p.second]){
cut_vertex.push_back(p.second);
used[p.second] = true;
}
if(p == (pair<int, int>){u, v}) break;
}
const int block_id = (int)bctree.size();
bctree.push_back(vector<int>());
bcnodes.emplace_back(true, move(block));
for(const int ver : cut_vertex){
bctree[block_id].push_back(bcnode_id[ver]);
bctree[bcnode_id[ver]].push_back(block_id);
used[ver] = false;
}
}
void dfs(const int u, const int p, int& tm, bool *used,
stack<pair<int, int> >& st, vector<int>& bcnode_id){
ord[u] = low[u] = tm++;
bool multi_edge = false;
for(const int v : G[u]){
if(ord[v] < 0){
st.push({u, v});
dfs(v, u, tm, used, st, bcnode_id);
low[u] = min(low[u], low[v]);
if(ord[u] <= low[v]){
if(!art[u] && (p >= 0 || check(u))){
art[u] = true;
bcnode_id[u] = (int)bctree.size();
bctree.push_back(vector<int>());
bcnodes.emplace_back(false, vector<pair<int, int> >{{u, u}});
}
identify_block(u, v, used, st, bcnode_id);
}
}else if(v == p){
if(multi_edge){
st.push({u, v});
low[u] = min(low[u], ord[v]);
}else{
multi_edge = true;
}
}else if(ord[v] < ord[u]){
st.push({u, v});
low[u] = min(low[u], ord[v]);
}
}
}
public:
vector<vector<int> > G;
vector<bool> art;
struct bcnode {
bool isBlock; // true: block, false: cut
vector<pair<int, int> > component; // edge set
bcnode(bool _isBlock, vector<pair<int, int> >&& _component)
: isBlock(_isBlock), component(move(_component)){}
};
vector<vector<int> > bctree;
vector<bcnode> bcnodes;
Articulation(const int node_size)
: V(node_size), ord(V, -1), low(V), G(V), art(V, false){}
void add_edge(const int a, const int b){
G[a].push_back(b), G[b].push_back(a);
}
int solve(){
int tm = 0;
bool *used = new bool[V]();
stack<pair<int, int> > st;
vector<int> bcnode_id(V, -1); // bcnode_id[original vertex] = cut vertex;
for(int i = 0; i < V; ++i){
if(ord[i] < 0) dfs(i, -1, tm, used, st, bcnode_id);
if(G[i].empty()){
// isolated vertex
bctree.push_back(vector<int>());
bcnodes.emplace_back(true, vector<pair<int, int> >());
}
}
delete[] used;
return (int)bctree.size();
}
};
verify 用の問題
Codeforces : Tourists
提出コード
yukicoder : ふたりのDominator
提出コード
