Runge Kutta

コードについての説明

微分方程式を数値的に解く手法. 正確には時間発展する未知の関数 $y(t)$ について $1$ 次の微分方程式 $dy / dt = f(t, y)$ および初期値 $y(t_0) = y_0$ が与えられているときに $y(t)$ を求める手法である. 解の存在および一意性を保証したいので $f(t, y)$ のリプシッツ連続性は仮定しておく.
ここで最もよく使われる $4$ 次のルンゲクッタ法について結論から言うと $i$ ステップ目の更新において

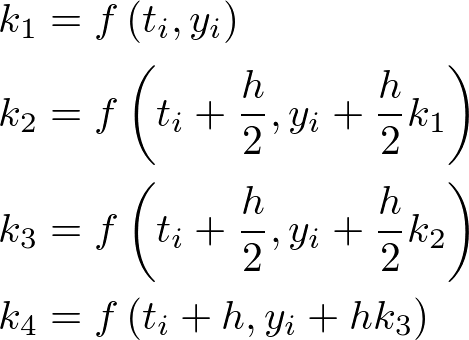
として、

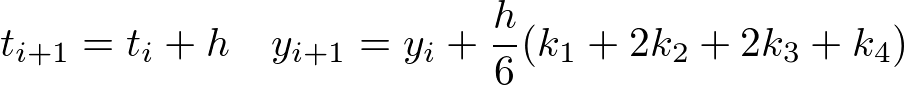
のように更新すると良い($h$ は刻み幅である).
オイラー法と違い、 接線の傾きである $k_1$ だけでなく $k_2, k_3, k_4$ を合わせて計算し, 加重平均を取ることでより正確に更新を行っている. このときテイラー展開を行ったとときの $4$ 次の項までが一致していることが頑張って計算すると分かり(正直に言うと私はしていないです), $1$ ステップでの誤差は刻み幅 $h$ について $\O (h^5)$ とオイラー法の $\O (h^2)$ と比べて誤差に強いと言える. 全体での誤差はステップ数が $\O (h^{-1})$ なので $\O (h^4)$ である.
最後に適当な例として $dy / dt = y \cos t$, 初期値 $t_0 = 0$, $y_0 = 1$, 刻み幅 $h = 0.5$, ステップ数 $n = 20$ とした場合のオイラー法, ルンゲクッタ法, exact な値($y = \exp(\sin x))$ の関係をグラフに表したものを以下に示す.

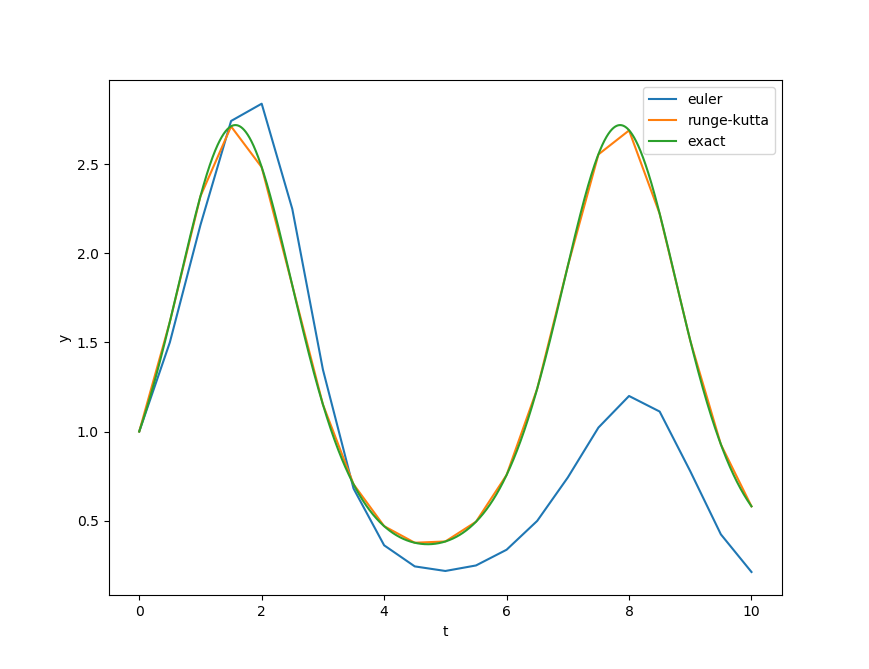
この例からはルンゲクッタ法の近似が良く, オイラー法の近似が悪いことが分かる.
大学での授業を参考に実装しました.

(関数)
runge-kutta$(t0, y0, h, n)$ : 引数は初期値 $(t0, y0)$, 刻み幅 $h$, ステップ数 $n$ で返り値は長さ $n+1$ の $(t_i, y_i)$ の vector.

時間計算量: $\O$($n \times$ (1 回の $f$ の計算量))

コード

double f(double t, double y)
{
    return y * cos(t);
}

pair<double, double> proceed(double t, double y, double h)
{
    double k1 = f(t, y);
    double k2 = f(t + h / 2, y + h / 2 * k1);
    double k3 = f(t + h / 2, y + h / 2 * k2);
    double k4 = f(t + h, y + h * k3);
    return make_pair(t + h, y + h * (k1 + 2 * (k2 + k3) + k4) / 6);
}

vector<pair<double, double> > runge_kutta(double t0, double y0, double h, double n)
{
    vector<pair<double, double> > result(n + 1);
    result[0] = {t0, y0};
    for(int i = 1; i <= n; ++i){
        result[i] = proceed(result[i-1].first, result[i-1].second, h);
    }
    return result;
}

verify 用の問題

verify していません(verify 問題を知らない)