高速メビウス変換(FMT)
コードについての説明
ゼータ変換(1), (2)の逆変換である. 包除と考えた方が良さそう.
(1) $s$ を含む上位集合 $T$ についての包除
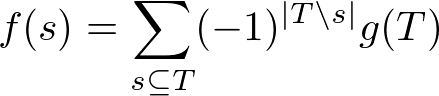
(2) $S$ に含まれる下位集合 $t$ についての包除

このとき $f$ は $g$ のメビウス変換でありこのような $f$ は計算量 $\O (n2^n)$ で求めることができ, 実装自体は以下のようにシンプルにかける(in-place で実装しているので少し分かりにくい).
(以下コードについて)
(1) については $i$ 周目の $g[j]$ は $j$ の下位 $i$ 桁以外一致しているような数 $k$ で $j$ を含むもの($j \subseteq k$) について包除を取っている.
$j$ の $i$ 桁目が $0$ のものについては $i$ 周目に更新する必要があるがそれは前の周までの $g[j | (1 << i)]$ を引いてやれば包除を取ることができる(賢い).
(2) については $i$ 周目の $g[j]$ は $j$ の下位 $i$ 桁以外一致しているような数 $k$ で $j$ に含まれるもの($k \subseteq j$) について包除を取っている.
$j$ の $i$ 桁目が $1$ のものについては $i$ 周目に更新する必要があるがそれは前の周までの $g[j \oplus (1 << i)]$ を引いてやれば包除を取ることができる.
時間計算量: $\O (n2^n)$
コード
// 上位集合(含む集合)を包除
void fast_mobius_transformation(int n, vector<int>& g)
{
for(int i = 0; i < n; ++i){
for(int j = 0; j < (1 << n); ++j){
if(!(j >> i & 1)) g[j] -= g[j ^ (1 << i)];
}
}
}
// 下位集合(含まれる集合)を包除
void fast_mobius_transformation(int n, vector<int>& g)
{
for(int i = 0; i < n; ++i){
for(int j = 0; j < (1 << n); ++j){
if(j >> i & 1) g[j] -= g[j ^ (1 << i)];
}
}
}
